
|
ConfrontoDistribuzioneIstogramma< Media pesata di dati con diverse varianze | Indice | Chi quadro e chi quadro ridotto > Confronto tra un istogramma e la distribuzione limite attesa Ritorniamo a considerare il risultato di una misura ripetuta di {$N$} valori, rappresentati per mezzo di un istogramma {$h(x_j)$}, con {$j=1,M$}, e intervalli {$\Delta x$}. Supponiamo di variare i parametri {$\mu$} e {$\sigma$} di una distribuzione normale {$P(x_j,\mu,\sigma)$} fino ad ottenere un ragionevole accordo tra il numero atteso, dato dal prodotto {$NP(x_j)\Delta x$}, e il numero di conteggi {$h_j=h(x_j)$} dell'istogramma. Come si valuta quantitativamente questo accordo? Il numero di conteggi sperimentali {$h_j$} può essere considerato un processo Poissoniano dal momento che è ottenuto con un numero {$N$} di misure che supponiamo relativamente elevato ed una probabilità di cadere nella colonna j-esima dato da {$P(x_j)\Delta x$} che è in genere molto minore di uno. Perciò la sua incertezza è pari alla radice del numero di conteggi, oppure, equivalentemente, dalla radice del numero atteso. 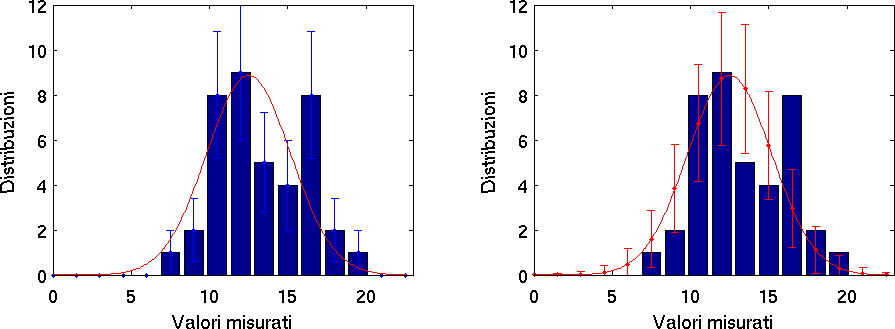 Istogramma dei risultati di {$N=40$} misure ripetute (colonne blu) confrontato con il numero di eventi atteso secondo la distribuzione normale (curva rossa). A destra le barre d'errore sul conteggio di ciascuna colonna sono date dalla radice di h, mentre a sinistra la barra d'errore su ciascun numero atteso è data dalla sua radice. Si vede che nella maggior parte dei casi l'accordo tra curva e istogramma è entro una barra d'errore, con entrambe le scelte. Una funzione matlab che produce un confronto simile a queste due figure, tra dati generati con incertezze normali e la loro distribuzione limite è scaricabile qui e si avvale di una funzione d'appoggio per calcolare il {$\chi^2$} e la sua probabilità. La funzione {$\chi^2$} quantifica l'accordo tra istogramma dei dati e distribuzione limite, valutando lo scarto tra {$h_j$} ed il numero atteso {$NP(x_j)\Delta x$}, nei termini delle loro incertezze: {$ (1) \qquad\qquad \chi^2 = \sum_{j=1}^M \frac {[h_j-NP(x_j)\Delta x]^2} {h_j}, $} oppure: {$ (2) \qquad\qquad \chi^2 = \sum_{j=1}^M \frac {[h_j-NP(x_j)\Delta x]^2} {NP(x_j)\Delta x}, $} Ricordiamo che a denominatore compare la varianza, il quadrato dell'incertezza sul numero di eventi. Per il processo Poissoniano che descrive il particolare numero di eventi nell'intervallo j-esimo si tratta del quadrato della radice, in definitiva il numero stesso di eventi. Questa varianza può essere stimata direttamente dal numero di conteggi sperimentale, come in (1), oppure utilizzando la distribuzione, come in (2). Le due scelte sono mostrate rispettivamente nella figura di sinistra e di destra. In matlab la distribuzione normale è ottenuta con
ed il suo integrale con
< Media pesata di dati con diverse varianze | Indice | Chi quadro e chi quadro ridotto > |