
|
Onde /
Stazionarie< Onde sulla corda | Indice | Battimenti > L'equazione di D'Alembert stabilisce la proporzionalità diretta (lineare) delle due derivate seconde parziali della funzione d'onda. Questo implica che se si hanno due possibili solufioni, ad esempio la fulzione {$h_1(x,t)$} e la funzione {$h_2(x,t)$}, allora qualunque loro sovrapposizione lineare {$$h(x,t)=a h_1(x,t) + b h_2(x,t)$$} è anch'essa una soluzione dell'equazione. Si controlla facilmente: la derivata della somma è la somma delle derivate. In termini fisici, due onde che si sovrappongono nello stesso spazio sono una onda composta. La somma di un qualunque numero di onde è anch'essa un'onda. Onde stazionarie Se si sommano un onda progressiva ed una regressiva di uguale ampiezza e frequenza si ottiene un onda stazionaria. Infatti {$$ A [\cos(\omega t - k x) + \cos(\omega t + k x)] = 2A \cos\omega t \cos kx$$} Il membro destro, come illustra la figura sottostante, è l'onda nera. Esso corrisponde al termine {$\cos kx$} con un'ampiezza {$2A\cos \omega t$} che oscilla nel tempo tra un valore positivo {$2A$} ed il suo opposto. Questa onda non si propaga: i suoi nodi (i punti rossi) restano fermi, ed anche le creste e i ventri pulsano su e giù, senza spostarsi. Il membro di sinisto è rappresentato dalle due onde rossa e blu, che invece si propagano nelle due direzioni opposte. Guardando con attenzione di intuisce che la loro somma produce ad ogni istante la corrispondente curva nera. 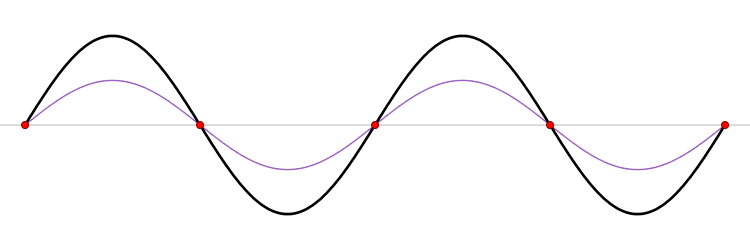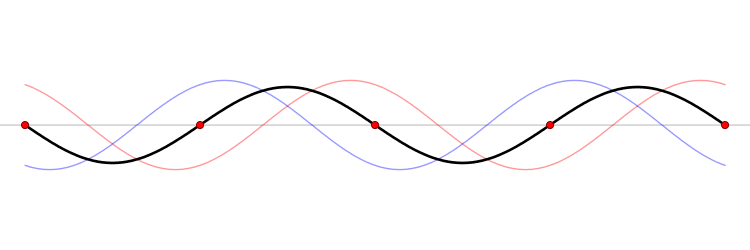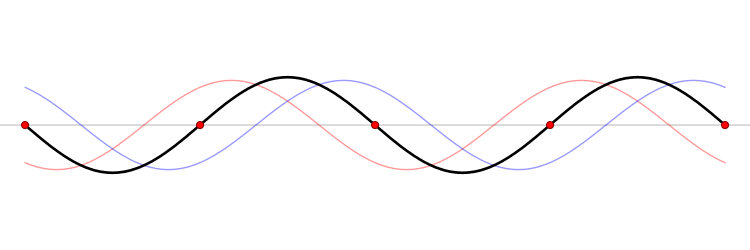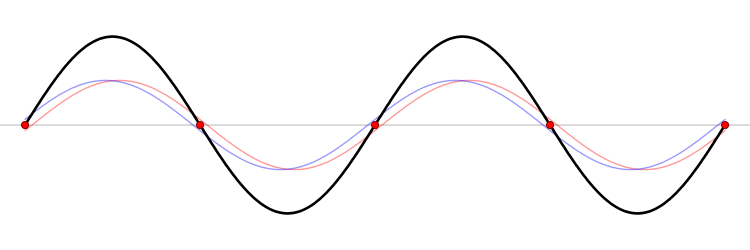 Da Wikipedia Si noti che nell'istante in cui l'onda somma nera ha ampiezza massima le due onde componenti coincidono. Questo è un esempio di interferenza costruttiva: due onde identiche, con la stessa fase si sommano dando un onda di ampiezza doppia. Viceversa nell'istante in cui l'onda somma nera è zero ovunque le due onde componenti sono opposte. Questo è un esempio di interferenza distruttiva: due onde identiche ma sfasate di {$\pi$} radianti si cancellano. Onde stazionarie sulla corda di chitarra Una corda di chitarra lunga {$l$} è fissata ai suoi estremi, che quindi non possono ondeggiare. Questi punti sono costretti ad essere nodi fissi dell'onda, ossia le uniche onde armoniche che possono esistere su una corda di chitarra (o di pianoforte, arpa, violino, ecc.) sono onde stazionarie. Le onde diverse sono in numero discreto, caratterizzato dal numero di nodi presenti sulla corda. L'onda principale, o fondamentale, che identificheremo col numero 0, ha solo i due estremi come nodi e quindi coincide con la metà di una sinusoide, la cui lunghezza d'onda deve essere pertanto {$\lambda_0=2l$} L'onda successiva, 1, ha un nodo in più, in mezzo alla corda. Pertanto la sua lunghezza d'onda è la lunghezza della corda, ossia {$\lambda_2=l=\lambda_0/2$}. L'onda con 2 nodi in più della fondamentale, ha lunghezza d'onda pari ai primi due terzi della corda, ossia {$\lambda_2=2l/3=\lambda_0/3$}. È facile controllare disegnando tre, quattro nodi equispaziati tra gli estremi che vale {$$\lambda_n=\frac{\lambda_0} {n+1}$$} Di conseguenza, siccome {$\nu=c/\lambda$} {$$\nu_n=(n+1)\frac c {\lambda_0} = (n+1) \nu_0$$} La vibrazione della corda impone all'aria, e quindi al timpano del nostro orecchio di vibrare con la medesima frequanza. Ogni frequanza corrisponde ad una nota. Di conseguenza il suono di una corda che vibra può essere costituito da diverse vibrazioni armoniche (le armoniche, in breve), La prima armonica ha frequenza doppia della fondamentale, e coincide con la stessa nota della ottava superiore. La seconda armonica ha frequenza tripla e così via. La foto mostra la prima armonica (l'ordinale corrisponde al numero di nodi interni) in vibrazione su una corda.  Onda stazionaria: la vibrazione della prima armonica della corda. Si intravede il trucco con cui la si è ottenuta < Onde sulla corda | Indice | Battimenti > |