
|
Onde /
Battimenti< Onde stazionarie | Indice | Principio di Huygens > Due onde sonore di uguale ampiezza e di frequenza leggermente diversa, {$\omega_1<\omega_2$}, arrivano al nostro orecchio. Consideriamo {$x=0$} la posizione del timpano. Il suono che l'orecchio percepisce è composto quindi da {$$A\cos\omega_1 t + A\cos\omega_2 t $$} Conviene definire la frequenza media {$\overline{\omega}=\frac 1 2 (\omega_+\omega_2)$} e la semidifferenza {$\Delta \omega= \frac 1 2 (\omega_2 -\omega_1)\ll\overline\omega$}, in modo che si abbia {$$ \omega_1 = \overline\omega - \Delta\omega, \qquad \omega_2 = \overline\omega + \Delta\omega$$} e quindi il suono composto risulta {$$A\cos\omega_1 t + A\cos\omega_2 t = 2A\cos\overline\omega t\cos\Delta \omega t $$} Siccome l'orecchio non percepisce come suono le frequenze inferiori a qualche decina di Hz questa combinazione, per {$\Delta\omega<10$} Hz si sente come una modulazione di ampiezza {$2A\cos\Delta \omega t$} di un suono a frequenza media (difficimente distinguibile da ciascuna delle due note componenti, a loro volta quasi uguali tra loro). 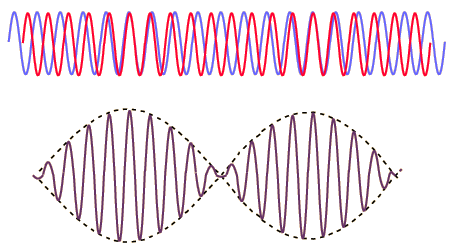 In alto le due onde, in blu la frequenza minore e in rosso la maggiore. In basso la loro somma. Figura presa da hyperphysics La figura mostra che i battimenti possono essere considerati un esempio di interferenza costruttiva e distruttiva. Considerando le due onde (quasi) della stessa frequenza, la frequenza media, per brevi tempi la differenza non si distingue, mentre su tempi più lunghi essa porta ad una differenza di fase tra le due onde, come si vede in alto. Quando sono (quasi) in fase si ha interferenza costruttiva e l'ampiezza dell'onda somma, in basso, è doppia. Quando le onde sono (quasi) in opposizione fase si ha interferenza distruttiva, ovvero il nodo dell'onda somma e il suono si annulla. L'orecchio (ossia il cervello) sente il suono delle frequenze al di sopra dei 20-30 Hz come note musicali pure. La frequenza media, {$\overline\omega$}, è una ben precisa nota, la nota principale. Se la frequenza {$\Delta \omega$} è di pochi Hz, non è un suono ed è interpretata come l'ampiezza della nota principale modulata nel tempo, {$a(t)=2A\cos\Delta\omega t$}, ovvero il suono {$a(t)\cos\overline{\omega}t$}. Nota che in un periodo di battimento il suono passa due volte da uno zero ad un massimo di intensità. Si può trovare qui una demo molto chiara del fenomeno: prova a produrre deu suoni alla stesa frequanza, due suoni di frequenze vicine e due suoni di frequenze sempre più diverse tra loro. Sentirai che i battimenti diventano più fitti. |