
|
Onde /
Interferenza< Riflessione totale | Indice | Diffrazione > Onda piana e raggio luminoso Il raggio di luce per eccellenza è quello che filtra da un forellino i una stanza scura e fumosa. ll raggio si vede lungo il suo percorso perchè le particelle di fumo lo riflettono da tutti i punti illuminati verso il nostro occhio, sfruttando la diffusione della luce. La luce è una piccola porzione dello spettro visibile, caratterizzata da llunghezze d'onda molto piccole, nell'intervallo in cui l'occhio umano è sensibile, {$\lambda_\text{blu}=4\,10^{-7}\le \lambda\le 7\,10^{-7}=\lambda_\text{rosso}$} m. Con lunghezze d'onda così corte in realtà il raggio di luce o il fascio sottile di un laser, che è facile immaginare come un fascio di raggi, è un'onda piana. Infatti la sezione del fascio, tipicamente di un mm2, ha dimensioni laterali 1000 volte maggiori della lunghezza d'onda, ossia della separazione tra i fronti d'onda. Interferenza di due sorgenti puntiformi L'interferenza si basa sul fatto che due onde che si sovrappongono, a seconda della loro differenza di fase, possono produrre un'onda con ampiezza somma delle loro ampiezze individuali, ma anche con ampiezza differenza o con uno dei valori intermedi. Ne abbiamo già descritti due esempi, discutendo l'onda stazionaria e i battimenti. Vediamo ora come evidenziare il fenomeno più direttamente. Consideriamo due sorgenti puntiformi (ossia di dimensioni minori della lunghezza d'onda). Un modo per ottenerle è di far incidere un'onda piana su uno schermo che la assorbe completamente, tranne che per due piccole apertura minori di {$\lambda$}, separate da una distanza {$d>\lambda$}, come mostrato nella parte superiore della figura. Lo stesso fenomeno si verifica con luce, onde sull'acqua, suono. Cambia la scala del disegno, deteminata da {$\lambda$}.  Ondoscopio: simulazione di una vasca d'acqua con un molo rosso che contiene due aperture, con illuminazione azzurra radente. Le bande nere e azzurre sono le ombre dell'onda e la loro separazione sono i fronti d'onda, separati da una lunghezza d'onda. Dall'alto incide un onda piana, mentre sotto le aperture si vedono le due onde sferiche che emergono molto vicino ai varchi. Più in basso si vede che l'interferenza distruttiva tra le due onde determina direzioni in cui l'ampiezza dell'onda (il contrasto tra azzurro e grigio) è minima. Calcolo delle direzioni Si può facilmente calcolare in che direzione cercare l'interferenza distruttiva, sfruttando il disegno qui sotto 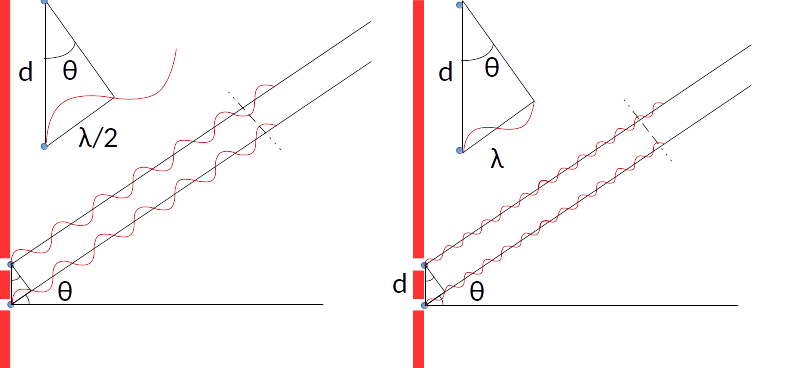 Cammini di due raggi emessi dalle sorgenti di Huygens in ciascuna delle due fenditure: a sinistra caso dell'nterferenza distruttiva, a destra caso dell'interferenza costruttiva (non in scala per chiarezza nel disegno: se la lunghezza d'onda fosse la stessa che a sinistra, l'angolo sarebbe maggiore) Immaginiamo che lo schermo sia a grande didtanza sulla destra. I due raggi (quasi) paralleli si incontreranno in un punto, identificato dall'angolo {$\theta$} e interferiranno distruttivamente nel caso di sinistra, perchè le onde, che partono in fase dalle due fenditure, viaggiano sfasate di {$\pi$} (opposte in fase). il tratto iniziale del raggio inferiore, che è Come si vede dal disegno questa condizione si ottiene richiedendo che la differenza di cammino {$\Delta r$} tra i due raggi sia pari a mezza lunghezza d'onda. La differenza {$\Delta r$} si ottiene proiettando la perpendicolare ai raggi dalla fenditura superiore, ossia costruendo il triangolo rettangolo riportato anche in alto. Da questo si ricava che {$d\sin\theta=\Delta r = \lambda/2$}. Con ragionamento analogo dalla figura di destra si ricava che i raggi sono in fase, ossia interferiscono costruttivamente se la differenza di cammino vale {$d\sin\theta=\Delta r = \lambda$}. Per ottenere questa condizione con la stessa {$\lambda$} occorre ovviamente che i raggi siano più inclinati di quanto mostrato in figura. Si realizzano così le direzioni di interferenza distruttiva e costruttiva visibili nell'immagine dell'ondoscopio. Nell'immagine dell'ondoscopio si vedono ben quattro angoli di interferenza distruttiva, due a destra e due a sinistra della verticale. Infatti se la differenza di cammino è un multiplo dispari di mezze lunghezze d'onda i raggi saranno ancora in opposizione di fase. Quindi le condizioni di interferenza distruttiva sono {$$\sin \theta = \pm (2n +1)\frac \lambda {2d}$$} a patto che {$\theta$} sia in valore assoluto minore di {$\pi/2$} Analogamente ci saranno più massimi, tra un minimo e il successivo, per {$$ \sin \theta = \pm n \frac \lambda {d}$$} con la medesima condizione di sopra. < Riflessione totale | Indice | Diffrazione > |