PmWikiFisica | Onde / Corda browse

< Equazione delle onde | Indice | Onde stazionarie >

Ora ci proponiamo di mostrare che una corda, sottoposta ad una tensione costante {$\tau$}, sostiene onde (è facile vederlo con un lungo filo steso, con la corda di una chitarra, oppure con questo dimostratore), perchè la seconda legge della dinamica si trasforma nell'equazione di D'Alembert.

Corda tesa

Consideriamo un tratto infinitesimo di corda tesa, orizzontale e trascuriamo la forza peso, molto minore della tensione. Quando è in equilibrio è soggetto a una forza risultante nulla, ossia la tensione {$\tau$} applicata dal tratto di corda alla sua sinistra, verso sinistra, deve essere uguale alla stessa tensione applicata dal tratto di corda alla sua destra, verso destra, come in figura a). Questo coincide con la definizione di tensione.

Immaginiamo lo stesso tratto deformato verso l'alto, come in figura b), che rappresenta solo una porzione della forma sinusoidale della corda. Chiameremo funzione d'onda l'altezza {$h(x,t)$} rispetto alla corda in equilibrio. È chiaro che {$h$} dipende da {$x$} perché la corda si curva, e anche da {$t$} perché l'onda, quindi la curvatura, si propaga lungo la corda.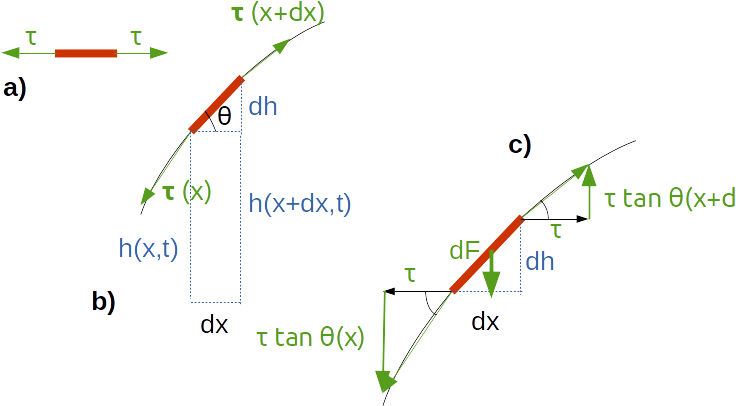

a) tratto infinitesimo di corda tesa in equilibrio; b) istantanea di una porzione di onda sulla corda, con il tratto infinitesimo {$dx$} soggetto a due tensioni non più esattamente opposte, per via della curvatura della corda; c) calcolo della la forza (infinitesima) risultante {$dF = dF_y$} sul tratto infinitesimo {$dx$} di corda.

Per applicare la II legge di Newton al tratto infinitesimo {$dx$}, che sarà {$dF_y = dm \,a_y$}, occorre fare le seguenti econsiderazioni:

la componente orizzontale della tensione deve rimanere equilibrata per garantire che il tratto di corda sia accelerato solo verso l'alto o il basso (stiamo considerando un'onda trasversale, che fa oscillare la corda solo in su o in giù);
la corda è omogenea, ossia ha una densità uniforme di massa ({$m$}) per unità di lughezza ({$l$}), che chiameremo {$\mu=m/l$}, e quindi il suo tratto infinitesimo ha massa {$dm=\mu dx$};
l'accelerazione verticale è la derivata seconda della coordinata verticale e coincide con

{$$\begin{equation} dm \, a_y(x) = \mu dx \, \frac {\partial^2 h}{\partial t^2}\end{equation}$$}

Inoltre dalla figura b) si vede che

{$$dh = h(x+dx,t) - h(x,t) = dx \tan \theta$$}

Nell'ultimo passaggio abbiamo fatto riferimento al triangolo rettangolo della figura b), in cui il cateto {$dh$} è uguale alla tangente dell'angolo opposto {$\theta$} per il cateto adiacente {$dx$}.

Per la funzione di una sola variabile, {$x$}, questa quantità sarebbe (al primo ordine in {$dx$}) pari a {$dh = dh/dx\, dx$}. Per la funzione di due variabili {$h(x,t)$} diventa

{$$dh = \frac {\partial h}{\partial x} dx = dx \tan\theta$$}

ossia dal secondo e dal terzo membro {$\tan \theta(x,t) = \partial h(x,t)/\partial x$}.

Ora la figura c) mostra che la risultante delle due tensioni, se si impone che le due componenti orizzontali siano uguali ed opposte, è {$\tau [\tan\theta(x+dx)-\tan\theta(x)]$}. Riproducendo il ragionamento fatto sopra questa differenza si può ricondurre alla derivata parziale della funzione {$\tan\theta(x,t)$}

{$$\begin{equation}dF_y=d\tau = \tau \frac {\partial \tan \theta }{\partial x} dx = \tau \frac {\partial^2 h}{\partial x^2} dx\end{equation}$$}

Nell'ultimo passaggio abbiamo trascritto la tangente di {$\theta$} come derivata parziale della funzione d'onda e abbiamo riconosciuto così la sua derivata parziale seconda.

Siamo ora in grado di ricostruire la seconda legge di Newton, dalle equazioni 1 e 2

{$$\tau \frac {\partial^2 h}{\partial x^2} dx = \mu dx \frac {\partial^2 h}{\partial t^2}$$}

Semplificando {$dx$} al secondo e terzo membro si riconosce l'equazione di D'Alembert per {$h$}

{$$ \begin{equation}c^2 \frac {\partial^2 h}{\partial x^2} = \frac {\partial^2 h}{\partial t^2}\end{equation}$$}

con

{$$\begin{equation} c=\sqrt{\frac \tau \mu}\end{equation}$$}

Controlleremo questo risultato alla fine della prossima pagina. Notiamo infine che un altro esempio dell'equazione di D'Alembert si ottiene discutendo le onde di densità o di pressione nella pagina Termondinamica, suono.

Strumenti a corda

Una chitarra, un violino, un pianoforte sono costituiti da corde tese, messe in vibrazione pizzicandole, strofinandole o percuotendole in un punto. Ciò genera un'onda stazionaria ? sulla corda, che mette in vibrazione l'aria circostante. La cassa armonica (il corpo della chitarra, del violino o del pianoforte) entrano in vibrazione a loro volta, rafforzando l'ampiezza delle onde sonore che si propagano nell'aria. La frequenza del suono che si propaga nell'aria è quindi la stessa dell'onda che viaggia sulla corda ed è imposta dai modi di vibrare propri di una corda, detti armoniche.

L'onda è stazionaria perchè è costretta ad avere nodi ai suoi estremi e, come si è visto, ciò è garantito dalla differenza di un'onda regressiva e di un'onda progressiva

{$$ h(x,t) = h_0[\sin(\omega t + kx) - \sin(\omega t - kx)] = 2\cos\omega t \sin kx$$}

Questo modo di vibrazione è l'armonica principale, di frequenza {$\nu_0=c\lambda_0$}. La velocità di fase, come si è visto, è fissata dalla tensione e dalla massa per metro della corda e la lunghezza d'onda è fissata dalla presenza di due nodi agli estremi: la lunghezza d'onda, come mostra la figura, è {$\lambda_0=2 l$}, il doppio della lunghezza della corda.

Ci sono però altri modi per garantire che gli estremi della corda siano fissi, come impone la costruzione dello strumento: sono tutte le onde stazionarie mosate in figura, che hanno 1, 2, 3, ..., n nodi ulteriori tra gli estremi. Essi hanno diverse relazioni tra lunghezza d'onda e lunghezza della corda. È facile vedere che, con n nodi a gli estremi (n + 2, inclusi i nodi agli estremi) la lunghezza d'onda è {$\lambda_n = 2l/n = \lambda_0/ n$}. Di conseguenza la frequenza risulta essere {$\nu_n = n \nu_0$}.

Generalmente il pizzico della corda genera un suono complesso che contiene sia l'armonica principale, sia le armoniche superiori ({$n\ge 1$}), sppure con ampiezza minore. Un metodo per generare prevalentemente la prima armonica (sopprimere l'armonica principale) è di tenere un dito appoggiato, senza premere, al centro della corda: ciò impedisce la vibrazione di ampiezza massima al centro (ossia tutte le armoniche pari), mentre consente le vibrazioni di armonica dispari, che hanno un nodo in quel punto. Come ad esempio nella canzone.

Attach:armoniche.png Δ

Fig. 1 Modi di vibrazione di una corda fissa agli estremi, indicati attraverso il numero di nodi interni, n: dall'alto al basso l'armonica principale, n=0, la prima armonica, n=1, la seconda armonica, n=2, eccetera.

< Equazione delle onde | Indice | Onde stazionarie >