
|
Onde /
Diffrazione< Interferenza | Indice | Potenza, ampiezza, intensitÓ di un onda > Diffrazione di una fenditura Vediamo innanzitutto come si presenta il fenomeno all'ondoscopio. Quando c'Ŕ una sola apertura (fenditura) nel molo, di dimensioni maggiori della lunghezza d'onda ma non troppo occorre immaginare pi¨ sorgenti di Huygens nel tratto di fronte d'onda che passa al di lÓ del molo. 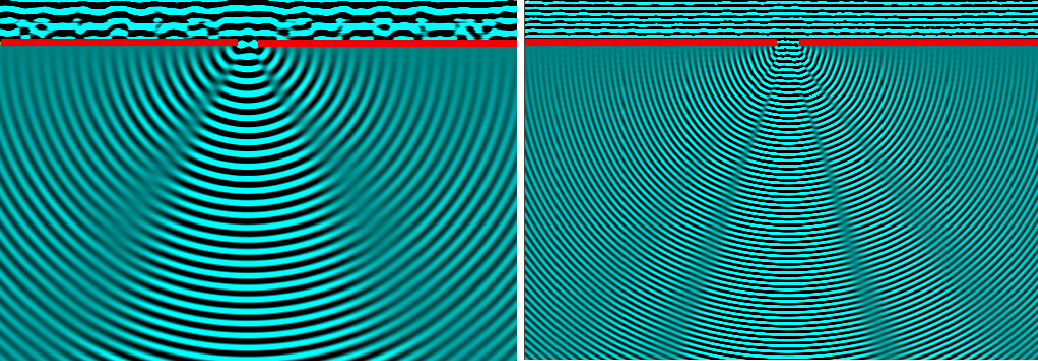 Quando la apertura {$a$} della fenditura Ŕ pi¨ grande della lunghezza d'onda le onde che emergono interferiscono tra loro. A sinistra {$\lambda\approx a/2$}: si vede un minimo di diffrazione per parte. A destra {$\lambda \approx a/4$} Ŕ pi¨ piccola, si vedono due minimi per parte e il primo minimo di diffrazione Ŕ and angoli minori. Si pu˛ calcolare a che angolo si trovano i minimi di diffrazione applicando un calcolo simile a quello visto per l'interferenza. SI cosiderano raggi paralleli in una data direzione, che si incontreranno a grande distanza sullo schermo in un punto. Occorre garantire che le sorgenti di Huygens, pi¨ di una e in numero arbitrario, interferiscano tutte distruttivamente tra di loro. A questo scopo conviene dividere in due parti uguali l'apertura. Come si vede dalla figura sottostante se si impone che la prima sorgente della prima metÓ interferisca distruttivamente con la prima della seconda metÓ, la stessa condizione garantisce che la seconda sia in opposizione di fase con la seconda, la terza con la terza e cosý via.  Raggi paralleli che partono dal fondo e da metÓ dell'apertura sono in opposizione di fase per un angolo tale che la differenza di cammino {$\Delta r$} sia metÓ lunghezza d'onda In questo modo per lo stesso angolo i raggi di tutte le sorgenti si cancellano a due a due. La condizione geometrica Ŕ mostrata nel triangolo in alto {$ \frac a 2 \sin\theta = \frac \lambda 2$}, ossia {$\sin \theta = \frac \lambda a$}. Se si considerano anche i possibili minimi successivi di intensitÓ si ottiene {$$ \sin \theta = n\frac \lambda a$$} a patto che {$\theta<\pi/2$}. Si nota dall'immagine dell'ondoscopio che per {$\theta= 0$} si ha un massimo di intensitÓ e che ci sono massimi secondari tra minimi successivi, ma, a differenza dell'interferenza tra due aperture puntiformi, l'intensitÓ dei massimi secondari Ŕ molto ridotta. Ci˛ avviene perchŔ, mentre per {$\theta=0$} tutti i raggi interferiscono costruttivamente, dando un'ampiezza pari alla somma delle ampiezze singole ed una intesitÓ pari al quadrato della somma (con {$n$} sorgenti di Huygens, ampiezza {$\propto n$} e intensitÓ {$\propto n^2$}), nei massimi secondari tutti i cammini sono differenti e le onde sono costrette ad interferire in parte distruttivamente. < Interferenza | Indice | Potenza, ampiezza, intensitÓ di un onda > |