• View
• Edit
• History
• Print

LimiteCentrale

< Chi quadro e chi quadro ridotto | Indice | Regressione Lineare >

Teorema del limite centrale

Il teorema del limite centrale attribuiscece uno status particolare alla distribuzione normale di probabilità. Infatti esso stabilisce che la distribuzione della somma di tante variabili casuali indipendenti tra loro, che seguano una qualunque distribuzione limite di probabilità con varianza finita, tende ad una distribuzione limite normale.

Non è il caso di fornire qui la dimostrazione di questo teorema, che fa parte di una serie di teoremi analoghi e più generali sulla variabili aleatorie (casuali). Chi fosse interessato può consultare l'articolo italiano della Wikipedia a riguardo (oppure l'articolo inglese).

Viceversa è immediato illustrare questo teorema con un esempio facile da riprodurre numericamente, con l'aiuto di matlab. Un esempio di distribuzione di probabilità ben diversa da quella normale è dato dal generatore di numeri pseudocasuali di base (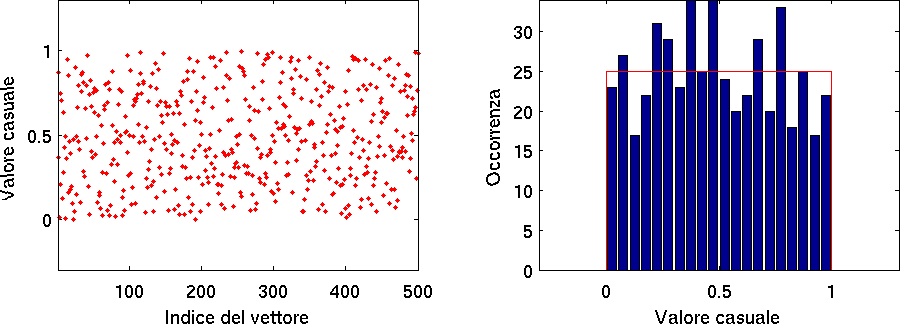rand(N,1), per matlab). La distribuzione limite di probabilità per questo generatore è costante nell'intervallo (0,1), e infatti il generatore produce numeri x distribuiti a caso in questo intervallo. Per provarlo basta ad esempio generare N=500 numeri casuali e farne il grafico, oppure, meglio, farne l'istogramma su intervalli di larghezza Δx=0.05, come nella seguente figura

Fig. 1 Grafico dei numeri casuali ottenuti con rand(N,1), N=500 (sinistra); l'ascissa è semplicemente la posizione nel vettore di numeri casuali generato da matlab. Istogramma dei dati (destra), con Δx=0.05; l'ordinata è il numero di valori casuali generati nell'intervallo corrispondente alla base della colonna e la linea rossa rappresenta la predizione della distribuzione attesa, con valor medio NΔx=25

La somma di due numeri casuali ottenuti con questo generatore dà invece il seguente risultato: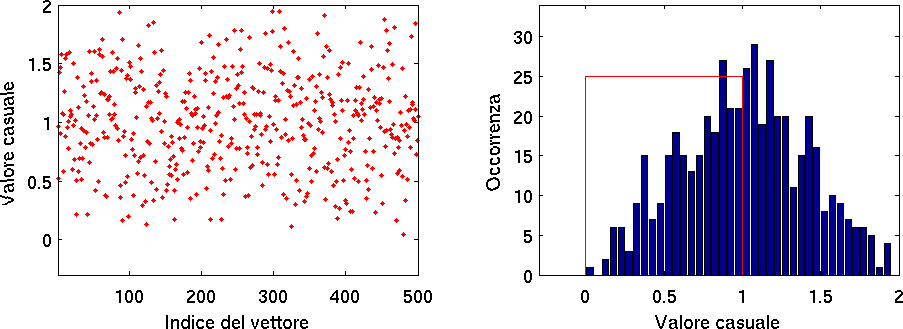

Fig. 2 Grafico dei numeri casuali ottenuti con sum(rand(N,2),2), N=500 (sinistra). Istogramma dei dati (destra), con Δx=0.05; l'ordinata è il numero di valori casuali generati nell'intervallo corrispondente alla base della colonna, la linea rossa rappresenta la predizione della distribuzione uniforme

La distribuzione è già notevolmente cambiata ed ha assunto un aspetto triangolare. È istruttivo ripetere il procedimento sommando progressivamente tre, quattro, otto numeri casuali. Mostriamo il risultato con la somma di M=12 numeri casuali uniformi.

Fig. 3 Grafico dei numeri casuali ottenuti con sum(rand(N,M),2), N=500, M=12 (sinistra); l'ascissa è semplicemente la posizione nel vettore di numeri casuali generato da matlab. Istogramma dei dati (destra), con Δx=0.05; l'ordinata è il numero di valori casuali generati nell'intervallo corrispondente alla base della colonna. Le due linee rosse rappresentano rispettivamente la predizione della distribuzione uniforme e quella di una distribuzione gaussiana di media 6 e deviazione standard 1.

Come calcolare valor medio e deviazione standard della distribuzione generata? Tenendo conto che si tratta della somma di numeri casuali di cui si conosce la distribuzione è facile calcolare questi due parametri con le regole della propagazione degli errori. Il risultato è esattamente μ=M/2 e σ=√M/12. Vediamolo, chiamando x i numeri casuali tra 0 ed 1 e y le loro somme.

Il valor medio per definizione vale {$\mu = \langle y \rangle = \sum_{i=1}^M \langle x \rangle = M \langle x \rangle$}. Il valor medio di x è facile da calcolare con la distribuzione limite uniforme, eq. (5). Siccome

{$\int_0^1 P dx=1,\qquad \mbox{\rm ossia} \qquad P=1$},

si ottiene:

{$\langle x \rangle=\int_0^1 x dx = \left[\frac {x^2} 2 \right]_0^1= \frac 1 2$}

e quindi {$\mu =M/2$}

La distribuzione approssima chiaramente la distribuzione normale, con il vincolo che non contiene, per costruzione, numeri minori di zero e maggiori di M.

< Chi quadro e chi quadro ridotto | Indice | Regressione Lineare >