Urto2D

Immaginiamo l'urto elastico tra due palle uguali (sfere di uguale massa m e raggio r) di cui una in moto con velocità v e l'altra ferma. Nell'istante dell'urto il parametro che determina le due velocità dopo è la distanza tra la seconda palla e la retta d'azione della quantità di moto della prima palla (parametro d'urto, v. figura).

Conviene passare al sistema del centro di massa, che ha velocità {$V=mv/2m=v/2$}. La conservazione dell'energia cinetica impone che entrambi i moduli delle due velocità dopo l'urto restino v/2, e cambi solo la direzione. La conservazione quantità di moto totale, nulla in questo riferimento, impone che le due palle emergano dall'urto in direzioni opposte. Infine, le componenti della quantità di moto delle due palle nella direzione normale (v. figura) si scambiano e quelle nella direzione tangente restano invariate (riflessione speculare). Chiamiamo {$u_x = - v/2 \cos2\theta$} e {$u_y =v/2 \sin 2\theta$} le componenti delle velicità dopo l'urto della palla in movimento. Per la seconda palla basta capovolgere entrambe le componenti.

Per ritornare al sistema di riferimento del laboratorio occorre sommare la velocità del centro di massa

{$ \begin{eqnarray*} v_{1x} &=& \frac v 2 \left ( 1-\cos^2\theta+\sin^2\theta\right) &=& v\sin^2\theta \\ v_{1y} &=& \frac v 2 2\sin\theta\cos\theta &=& v\sin\theta\cos\theta \\ v_{2x} &=& \frac v 2 \left ( 1+\cos^2\theta-\sin^2\theta \right)&=& v\cos^2\theta \\ v_{2y} &=& - \frac v 2 2\sin\theta\cos\theta &=& - v\sin\theta\cos\theta \end{eqnarray*} $}

Il triangolo rettangolo ha come ipotenusa la distanza tra i centri, pari a 2r, e come cateto il parametro d'urto d. Quindi l'angolo θ vale asin(d/2r). Se passiamo nel sistema del centro di massa vale lo stesso disegno, ma la palla si sinistra si muove verso destra con componente orizzontale della velocità -v/2 e la palla di destra si muove verso sinistra con componente orizzontale della velocità v/2. Come spiegato nel testo avviene un urto speculare: gli angoli di riflessione sono uguali agli angoli di incidenza, rispetto alla direzione normale congiungente i due centri.

In definitiva l'angolo tra la velocità iniziale e finale della prima palla nel laboratorio è

{$$ \phi= \tan^{-1} \frac {v_{1y}} {v_{1x}} = \tan^{-1} \frac {\cos\theta} {\sin\theta}= \frac \pi 2 - \theta $$}

mentre l'angolo tra la velocità iniziale della prima palla e la velocità finale della seconda palla (quella inizialmente ferma) è

{$$ \phi^{'}= \tan^{-1} \frac {v_{2y}} {v_{2x}} = \tan^{-1} \frac {\sin\theta} {\cos\theta}= \theta $$}

In questo caso particolare si vede che nel laboratorio la componente tangente del momento lineare di ciascuna palla resta invariata e quella normale si comporta come nell'urto in una dimensione (siccome le masse sono uguali la prima palla perde quella componente e la acquista la seconda). Si vede facilmente che queste due affermazioni sono vere anche nel centro di massa e sono vere anche nel caso elastico generale (masse e velocità iniziali differenti)

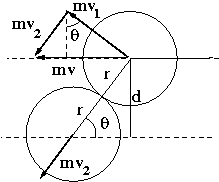
Urto nel laboratorio: il momento lineare iniziale è scomposto nella direzione tangenziale e normale. Le due componenti coincidono con i momenti della prima e della seconda palla dopo l'urto.