
|
EserciziLezioneDue< Esempio della scimmia | Indice | Dinamica del punto materiale >
Occorre disegnare due vettori di lunghezza differente che formano un angolo generico (non retto). Si ottiene il vettore somma con la regola del parallelogrammo. 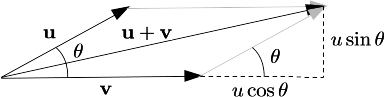 Si nota che la replica grigia di {$\mathbf u$} ha proiezione lungo {$\mathbf v$} pari {$u\cos\theta$} (linea tratteggiata orizzontale). Viceversa la proiezione perpendicolare a {$\mathbf v$} vale {$u\sin\theta$} (linea tratteggiata verticale). Risulta inoltre che {$\mathbf v+\mathbf u$} è l'ipotenusa di un triangolo rettangolo di cateti {$u\sin\theta$} e {$v+ u\cos\theta$}. Quindi applicando il teorema di Pitagora si può calcolare {$$ u+v = \sqrt{u^2 + v^2 + 2uv\cos\theta}$$}
Applicando il teorema del coseno {$$ \theta = \cos^{-1} \frac {w^2-u^2-v^2}{2uv}$$}
Di nuovo conviene fare un disegno: 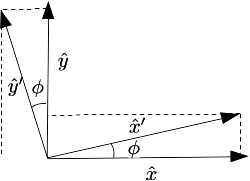 Le righe tratteggiate indicano le proiezioni dei versori {$\hat x^\prime, \hat y^\prime$} sui versori {$\hat x, \hat y$}. Si vede immediatamente che {$$\begin{align*}\hat x^\prime &= \cos\phi \hat x + \sin \phi \hat y\\\hat y^\prime &= -\sin\phi \hat x + \cos \phi \hat y\end{align*}$$}
{$$cos^2\alpha+\cos^2\beta+\cos^2\gamma =1$$} Questa relazione fa pensare immediatamente al modulo del vettore {$\mathbf v$}, che vale {$v=\sqrt{v_x^2+v_y^2+v_z^2}$}. Infatti, siccome {$v_x$} è la proiezione ortogonale di {$\mathbf v$} su {$\hat i$}, {$v_y$} su {$\hat j$} e {$v_z$} su {$\hat k$} si avrà {$$v_x = v\cos\alpha, \quad v_y = v\cos\beta, \quad v_y = v\cos\gamma$$} Quindi si può scrivere {$$ v^2 = v_x^2+v_y^2+v_z^2 = v^2(cos^2\alpha+\cos^2\beta+\cos^2\gamma)$$} da cui scende immediatamente la relazione cercata. < Esempio della scimmia | Indice | Dinamica del punto materiale > |