• View
• Edit
• History
• Print

MolecularMagnet

< Muzen: a FORTRAN 77 & c analysis program (historical) | Index | MuSR.Polaron >

Hypothesis on a radical state in a skeleton molecular magnet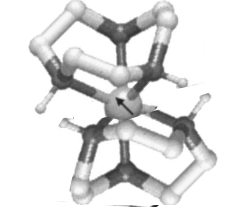

This molecule is a hypothetical(?) unit of (tecn)₂Fe (see Fe8). Suppose that Fe is Fe²⁺ (probably a chemical heresy). Muon will attach to a {$C=C$} and make a radical with one unpaired electron, {$\cdot C-C-Mu$}. The Hamiltonian of this complex radical will be:

{$ \frac {\cal H} h = -\Gamma B S_z - \gamma_e B s_z + \gamma_\mu B I_z -\gamma_e\gamma_\mu \mbox{\it\bf s}\cdot\nu_{sI}\cdot \mbox{\it\bf I} + \Gamma\gamma_e \mbox{\it\bf S}\cdot\nu_{Ss}\cdot \mbox{\it\bf s} - \Gamma\gamma_\mu \mbox{\it\bf S}\cdot\nu_{SI}\cdot \mbox{\it\bf I} + \sum_n {\cal H}_n $}

where {$\Gamma,\gamma_e,\gamma_\mu$} and {S,s,I} are magnetogyric ratios and spin operators of Fe, the unpaired electron and the muon, respectively, {$ \nu_{sI}, \nu_{Ss}, \nu_{SI}$} are the electron-muon, Fe-electron, Fe-muon hyperfine frequencies, and the interactions with the other nuclei are grouped in the last sum, which contains likewise a Zeeman and two hyperfine terms with frequencies {$ \nu_{sn}, \nu_{Sn}$} per each of the six H. ¹⁴N is neglected for its low magnetogyric ration and ¹³C for its low abundance.

The Paschen-Back regime (decoupling of all spins) is reached in this case above the highest hyperfine field, {$B_0=\max(\nu_{sI}/\gamma_e,\nu_{SI}/\Gamma)$} (see e.g. muonium), and probably these two hyperfines are comparable (of order 0.02T).For reference, the Mu-cyclohedadienyl radical has a hyperfine field of the muon on the electron of about 0.018T, or euivalently of the electron on the muon of about 3.7T Chem . Phys. Lett. 57 (1978) 37

Proton hyperfines are much smaller , since the electron field on proton is of order 0.2T Phys. Rev. B 64 (2001) 094439) (the muon field on the electron is {$\frac {\gamma_p} {\gamma_e} = \frac 1 {206.6} $} as much, i.e. circa 10 G).

< Muzen: a FORTRAN 77 & c analysis program (historical) | Index | MuSR.Polaron >