
|
DecadimentoAlfa< Decadimento radioattivo | IntroduzioneFisicaMateria.Indice | Decadimento beta? > Le particelle {$\alpha$}, corrispondenti a nuclei di {$^4_2\mbox{He}$}, sono prodotte da decadimenti di isotopi instabili {$^A_Z \mbox{X}$} il cui difetto di massa è minore di quello di {$^{A-2}_{Z-2} \mbox{Y}$} più quello di {$^4_2\mbox{He}$}. Modello di Gamow Nel caso classico un particella alfa ci mette un tempo {$2R/v$} per transitare attraverso un nucleo di raggio {$R$}. I tempi di decadimento sono molto più lunghi. La spiegazione di Gamow è basata sull'effetto tunnel. Fuori la particella è un'onda piana che può assumere qualsiasi valore di energia cinetica {$\hbar^2k^2/2m$}. Nella buca rettangolare larga {$2R$} (modello lineare per semplicità) invece assume valori discreti di energia. Supponiamo che abbia uno stato fondamentale {$E$}. In questo stato è un'onda di vettor d'onda {$k_0=\sqrt{2m(U-E)}/\hbar$}. Se la barriera è larga {$L$}, la probabilità di tunneling vale {$$T=e^{-2k_0L}$$} e, se la barriera è larga, questa probabilità è molto piccola. Quindi la frequenza di emissione diventa la frequenza classica (freequenza dei tentativi) moltiplicata per {$T$}, molto miniore della frequenza classica. Il conto di Gamow (1928) è più raffinato. Immagina che la barriera, fuori, ha una coda Coulombiana, {$U(r)=2Ze^2/4\pi\varepsilon_0 r$} che fa variare {$k_0$} a seconda del valore di {$r$}. Ricordando che {$\log T = -2k_0 L$}, il calcolo viene affinato così, {$$ \log T = -2 \int_R^{r_0} k_0(r) dr$$} dove {$r_0=2Ze^2/4\pi\varepsilon_0 E$} è il valore più esterno della barriara, al quale {$U=E$}. Un conto dettagliato mostra che questo modellino è in accordo con i dati di Geiger e Nuttal del 1911. 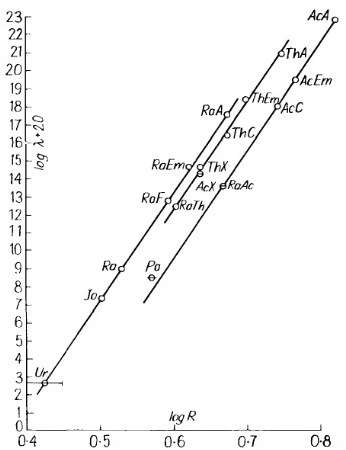 Tassi di decadimento {$\lambda=1/\tau$} per gli emettitori alfa noti all'epoca, con i loro nomi provvisori, in funzione della lunghezza di penetrazione in aria, misura della loro energia, proporzionale al quadrato della velocità. Siccome la velocità è proporzionale al tempo di transito, ci si attende classicamente una relazione lineare tra radice dell'energia e tasso di decadimento. Invece la relazione è esponenziale per via del fattore{$T$} dovuto all'effetto tunnel. < Decadimento radioattivo | IntroduzioneFisicaMateria.Indice | Decadimento beta? > |