
|
Hpc /
CrAsSummary Where to go (?) The results below indicate that NEB on V (Hartree potential, without muon) gives totally unreliable barriers. Reliable barriers require inclusion of the quantum muon (path integral, SCHA, thermal bath MD, ...). However
Therefore we may trust the QE NEB hierarchy: 1-2 is lowest, 1-3 and 1-4 are equivalet and higher. Summarising:
Todo: clarify the topology of the network. (*) The local field among all sites 1 in the same chain is identical since the k vector of the helix is orthogonal to c. In site 2 the field is equivalent but in principle with a different phase in the helix. Therefore there could be some moderate averaging with a motion restricted to the 1-2 chain. The 1-2 chain should be equivalent to the motion back and forth between the sites of a 1-2 dimer. We should quantify this with muesr (Anyi?). NEB, V potential vs. QE total energy In the following 1, 2, 3 and 4 are symmetry-equivalent sites for an incoming muon, but when the muon localizes in one of them it relaxes the lattice. Therefore the starting site with the muon becomes distinct from the other three in the QE total energy calculation. V is the Hartree Coulomb potential without the muon. The paths turn out to be the same but the former have more images (the NEB on V passes through the same images found by the NEB on QE). The paths look smoother and gently bent with V because of the greater number of images. We plot below QE total energy differences from the starting, relaxed muon position 1 to neighboring unrelaxed 2, 3, 4 ... positions (left) and the potential differences from the same starting position to the same final positions. ote that the cell positions are the same, but in the V case they do not correspond to a minimum and, as a matter of fact, the NEB relaxes first to the nearby minimum, then it climbs over the barrier to the other site.  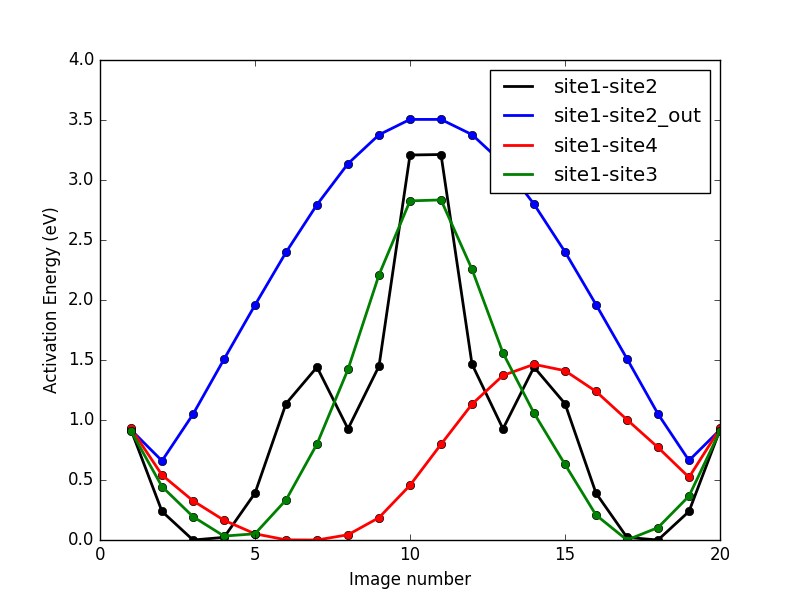 QE NEB (left) and V NEB (right) Considerations: Note that in the V plot starting and final sites are all equivalent by symmetry. Looking at the paths backward (from the final unrelaxed positions), we expect the landscape to be more similar between the two plots. However they are not: barrier energies differ by a large factor and even the hierarchy of the apparent activation energies is different in the two plot. The absolute starting site-1 energy value is expected to be very different in the two plots, on physical grounds (the QE value refers to the relaxed configuration, the V value is unrelaxed). However even a rough comparison of energy barriers must account for the deeper potential well at the starting relaxed site 1. In summary we cannot compare the barriers on the V plot. QE refines the following H sites (the lattice relaxed around a H in this site has absolute minimum total energy, site H1, or local minima of the total energy, sites H7, H8, H9)
There are two types of diffusion. The thermally activated diffusion contemplates jumps from a relaxed to a non relaxed lattice position. This model is valid if the residence time {$\tau_{\text{res}}\ll \tau_{\text{jump}}\approx \tau_{\text{phonons}}$}, where the second two time-scales are those characteristic of ballistic muon motion and lattice relaxation, respectively. This diffusion model assumes that the muon instantaneously jumps from a relaxed position to a non relaxed position, then the lattice relaxes and the muon spends a long {$\tau_{\text{res}}$} in it. The jump frequency is thermally activated, {$1/\tau_{\text{res}}(T) = \nu_\infty \exp(-T_a/T)$}. Quantum diffusion or hindered tunnelling requires instead that the non relaxed minima among which the motion occurs lie within a small energy difference {$\Delta E$}, and spatially separated by a distance comparable to the extent of the muon wave function (say, 0.5 Angstrom), so that the overlap between the wave function of muons located at the starting and final position is non negligible. This takes place for instance for H in methyl groups. The attached Vesta file shows paths among H1 sites and its symmetry replica (called 2, 3, 4 in the QE NEB calculations). The H1-2 sites are 2.5 A apart and form a zigzag chain along c. One may assume that H1 is relaxed and the other 2-1-2-1-2 sites of the chain are not. QE NEB shows a trajectory between 1 and 2 that has a single barrier in between ~0.5 eV high. The actual activation energy will be lower because of the muon Zero Point Energy. We can expect a thermally activated 1d motion along this network. No other path among these sites is expected. The QE NEB between 1 and 3 and 1 and 4 show crooked trajectories with higher barriers. The H7, H8 and H9 sites are less likely for this classical type of motion on the grounds that their total energy as a relaxed staring position is 0.4 eV higher than that of H1. However there is a H8-H7-H9-H7-H8 path where these relaxed positions are very close to each other both spatially (H7-h8 is 1.22 Angstrom and H7-H9 is 0.86 Angstrom) and in energy (within 0.14 eV of one another). Can they give rise to muon delocalization via tunneling? In order to address this question we should look at the non relaxed sites, the minima of the Hartree potential without the muon. In any case both tentative paths are along c and not connected in the ab plane. i.e. they give rise to a 1D type of muon diffusion along c. Since the q vector of the incommensurate helix is along a this 1D diffusion leads to no averaging and no relaxation. What is then producing relaxation?
|